纵使小编我高中数理化都学的很好,但这样的好基础对于帮我叩开统计学的大门却没提供什么帮助。被统计学教材上“天书”般的统计公式吓破胆之后,也就勉强能在软件的帮助下计算个被大家奉若神明的”P值”,但统计学界却要齐心协力将我这点仅有的统计学武功废掉。
虽然目前高考常被大家吐槽,但尚无更好的制度创新之前人才的选拔还得照这个路走下去。虽然统计学界觉得我等统计学小白把P值玩坏了,有些杂志甚至宣布不再发表含有P值的研究论文,但小编觉得推行其它更高级的统计学方法尚有难度,可行办法还是应该深入了解、学习P值,把P值用好。
先让我们跟随这篇文章了解一下P值到底是个什么东西:
《小白学统计系列之三:P值到底是个什么东西》 — — 冯国双 小白学统计
简单说一下P值的历史,P值是由统计学界最牛的人Fisher老先生(相当于物理领域的牛顿级别人物)提出并推动的,这来源于他以及以后由奈曼和皮尔逊发展的假设检验思想(假设检验会在以后文中专门介绍)。简单地说,如果你有一个50人的班级,已经知道你们班上50人的身高平均是170cm,如果现在给你1个人,身高是190cm,那么让你来判断,这个人是不是你们班的人?
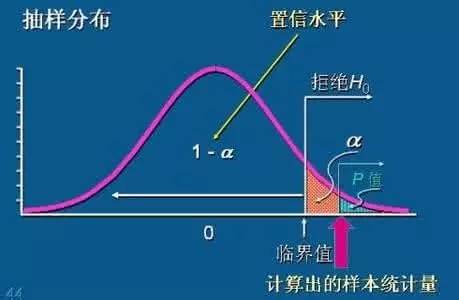
对于这个问题,你会怎么判断呢?很明显,两种答案,要么是,要么不是。通常我们会假定他是这个班上的人,因为即使是平均身高170cm,但也不是所有人都170cm,肯定有高有矮,高的人是有可能达到190cm的。但是我们不得不承认,对于一个平均身高是170cm的50人来说,出现一个190cm高的人,这种几率是相当低的。这个“几率”就是P值。
换句稍微专业一点的术语来说,对于一个均值是170cm的总体,有人的身高比均值高20cm,如果这个人真的是这个群体中的,那么出现20cm这么大的差异的概率有多大?这个概率就是P值。如果这个概率很小(如P值=0.01),那就可以说,出现这么大的差异的概率只有百分之一。对于这么小的概率,我们认为它不大可能出现,也就是说,这个人不大可能是属于这个群里中的,更大的可能是属于其他群体中的。
现在还面临一个问题,P值到底小于多少,我们才能下结论认为这个人不大可能属于这个群体呢?换句说话,小于多少才算“不大可能”?现在我们通用的标准是0.05,也就是说,概率小于5%,就认为“不大可能”。那这个0.05是怎么来的呢?这个0.05也是Fisher老先生提出来的,可是他没有对此做任何解释,只是说他突然想起来了,或许觉得0.05是他的幸运数字吧,然后就用0.05了,然后我们就一直沿用了。
不管0.05是Fisher老先生的一个偶然想法还是怎么样,起码我们真的就有了一个标准了。只要能统一,始终是好事的,尤其在以前的时候。不过在当前计算机已经超级发达的时代,有这么一个标准就不一定是好事了。很多人都曾有过这种经历,P值正好等于0.049或0.052之类的。等于0.049的,感觉神都在眷顾他;等于0.052的,恨不得一头去撞墙。也有人问过我,我的P值等于0.052,我可不可以四舍五入到0.05?
实际上,对于P值等于0.052之类的问题,也不用太烦恼。现在的杂志一般都要求提供具体的P值,而不是简单写为P<0.05等。为什么呢?因为P值仅仅告诉你,根据你的数据所得出的结论,有多大的犯错风险。P值是对已有的(注意是已经有了的)结果的判断,而不是反映了结果大小。比如刚才例子中,结果已经有了,就是差值是20cm,P值的作用是判断出现这么大的值到底有多大可能。对于0.052来说,比0.05多了千分之二的可能性,难道你觉得增加这千分之二的可能性可以让你推翻你的结论吗?我相信大多数人都不会这么认为。所以你大可不必纠结于想方设法非要改成小于0.05的事情,大大方方地把自己的P值放上,我想读者会有自己的判断的。如果一个杂志因为你的P值=0.052而拒绝承认你的结论,我想这个杂志也不值得发表。
目前仍有人认为P值代表了差异大小,认为P值越小,差异越大,因此力求一个小的P值。而事实上,P值跟差别大小没什么太大关系,真正有关的反而是其他因素,比如例数的多少,这是个很重要的因素。例数少的话,就容易出现一个大的P值。以前就有临床大夫质疑统计学,说:你看你们统计学,20个数据P值就大于0.05,我原封不动地复制成200个,P值就小于0.05,有统计学意义了。这不是在玩数字游戏吗?
我要说:你说的恰恰相反,20个数据时, P值大于0.05,不让你有统计学意义,是在给你一个提醒,说明你的数据不足以支持你的结论。就像是你治疗了20个人,即使都治好了,你如果宣称治愈率100%,估计没人会相信你。但是200个人就变成P值小于0.05,这正好说明了结论更可靠了,如果你对200个人治疗还是都治好了,那你这时候说治愈率100%,我相信一定会有更多的人相信你。所以,好好想想P值吧,它是有现实意义的。统计学不是数字游戏,而是让你的结论更有说服力。靠什么来体现你的结论的说服力呢,P值。
再来了解一下为何P值地位不保:
《P值“大佬”地位恐不保,统计学大牛齐发难》 — — 子非鱼 解螺旋
P值这个科研领域中神奇的数值,让无数人为之欢喜,为之悲伤。当P值成为衡量统计真实性的“黄金标准”后,就存在着无数方法在试图将其变得越小越好。而这种P值至上的做法无疑是现在科学论文无法被重复的原因之一,如今更是被诸多统计学大牛指出,P值远没有众多科学者想象的那么可靠,显然它在统计学的大佬地位已经岌岌可危。
P值,曾经统计学的王者
90年前P值自诞生后就一直饱受争议,有人形容它为讨人厌又赶不走的蚊子,也有人形容为存在明显问题但人人视而不见的皇帝新衣。但实际上, 1920 年英国统计学家Ronald Fisher 首次引入 P值时,仅仅是想将其当做判断所得的实验数据在传统意义上是否显著的非正式方法,而非决定性的检验方法。
而真正推动P值风靡全球的却是Fisher的竞争者波兰数学家Neyman及英国统计学家 Pearson ,当时他们提出另一种包含统计效能、假阳性、假阴性等概念的可替代的数据分析方法(该法直接忽视P值这个指标)。
至此,两个派系一直争执不下,却过早耗尽了其他研究者(非统计学家)的耐心。对两种算法均缺乏透彻理解的研究者粗略将P值融入了Neyman和Pearson 所建立的统计系统,就开创了一种新的混合统计方法——当P值<0.05,统计结果可视为显著。
而目前,许多科学领域中的研究结果的意义均是由P值来判断的。它们被用来证明或驳回一个“零假设”:通常假定所测试的效果并不存在。当P值越小,该实验结果就越不可能是由纯粹的偶然所造成的。
左右为难的P值
因而,为了追求所谓的显著性结果,不少研究者选择进行“P值操纵(P-hacking)”,即研究者在收集实验数据时,在没有假定一个“零假设”的前提下,却故意在实验结果中让P值达到可以发表的程度,而这也导致一些探索性研究结果,看似确定无疑,实际上却难以重复。
这也是为什么许多科研者会担忧P值会产生假阳性结果的原因所在。
其实近年来对P值的批评一直不断,2011年一些研究者就试图对这一问题提出警告,因为有人曾利用统计学分析得出结论:大学生听披头士乐队的音乐会变得更年轻。更令人争议的是,2015年一则记录片揭露了一项基于P值的低劣临床试验是如何得出了荒谬的结果——吃巧克力可以减肥(目前该文章已被撤回)。
因而对于P值滥用的情况,2016年美国统计学会(AmericanStatistical Association,ASA)就曾发表声明呼吁研究者们要慎用P值,不要仅是基于P值而做出科学结论或政策决定,而是要对具有统计显著意义的结果进行数据分析描述,还应对所有统计试验以及计算中做出的选择进行合理解释,否则结果很有可能看起来不可靠。
改造P值,降低阈值
另外,为了增加P值的可信性,7月22日所发表在PsyArXiv预印服务器上的一篇质疑P值的文章指出,生物医学科学论文结果的p值阈值应该降低到0.005,即P<0.005才算是统计上有显著差异。且该论文即将被发表在Nature Human Behavior杂志上。
而之所以将阈值定为0.005,文章指出该阈值与贝叶斯因子为14-26的效果相对应,是衡量实验数据真实有效的强力证据;且该阈值在很多研究领域能够较好的控制假阳性结果的产生。
洛杉矶南加州大学的经济学家以及该论文的合著者Daniel Benjamin表示:“研究者根本就没有意识到,当P值为0.05时,这份证据的可靠性到底有多弱。”同时,他还认为处于0.05到0.005之间的P值只应被视为“提示性证据”而非既定知识。
降低阈值≠一劳永逸
难道降低P值阈值后就能高枕无忧了么?其实不然,荷兰格罗宁根大学的心理测量统计研究员Casper Albers认为如此的做法反而引起了另一个问题:它可能会增加实验中假阴性的几率。
为了解决这个问题,Benjamin及其同事建议研究人员将样本量增加70%,如此不仅能降低假阴性率,同时还能显著降低虚假结果出现的概率。但Albers认为,实际上只有资金充足的科学家才能有办法做到这一点。
英国雷丁大学的认知神经学家TomJohnstone说,降低p值阈值还有可能会加剧“抽屉问题(file-drawer problem)”,即统计结果显著的文章更容易出版,而可能同样重要的非显著结果则锁在抽屉里,别人永远无法看到。对此,Benjamin的看法是,无论P值结果如何,所有的研究结果都应该公之于众。
芝加哥伊利诺理工大学的计算机科学家Shlomo Argamon表示,这个问题没有简单的解决方案,因为无论你如何选择置信区间,在通过足够多的不同实验设计来验证结果时,很可能会出现至少一次实验偶然地给出统计学显著结果。
P值的解决之道
虽然P值问题一直存在,但是相关统计学上的改进措施依然进展缓慢。针对此情况,Argamon指出现阶段,在数据统计方面上,需要进行彻底的变革——人们必须改变统计学的教授方式、数据分析方式以及结果呈现和解释方式,比如研发一种新的统计方法标准以及一系列研究激励措施。
考虑到P值<0.05会导致更多假阳性结果,德克萨斯A&M大学的统计学家Valen Johnson指出,从原子碰撞实验中收集大量数据的粒子物理学家一直都要求P值要低于0.0000003(或3×10−7 )。
而十多年前,遗传学家采取了类似的措施,在进行全基因组关联研究来寻找不同人群中疾病与DNA突变体之间联系时,要求P值要小于5×10−8。
而有些科学家却已然放弃了P值,转而青睐更为复杂的统计学工具,如贝叶斯检验(Bayesian test),此方法会需要研究人员来定义和检测两个替代假设,虽然并不是所有的研究人员都有专业技术进行Bayesian test。
甚至已有一些的科学领域开始对P值进行打压。2015年,心理学杂志 Basic and Applied Social Psychology (BASP) 就已经宣布将不再发表含有P值的研究论文。
另外,还有些研究者则赞成一种更普遍的方法,即鼓励研究者对同一套数据用多种方法进行分析。Johnson也认为,P值本身并非邪恶,它对于判断一个假设是否得到证据支持仍然有用。
最后为大家奉上美国统计学会(ASA)发布的6条P值使用原则:
1. P值可以表示数据与一个特定的统计模型是否相容
例如在零假设通常用来假设一个效应不存在,如两组之间没有差异,两个因素没有相关性。此时P值越小,数据与零假设的不相容性(incompatibility)越大,可以解释为这些数据怀疑或否定了零假设。
2. P值不能代表假说为真的概率,也不代表数据完全是由随机因素造成的概率
P值是所得数据与解释之间关系的说明,而不是对解释本身的说明。
3. 科研结论、商业决定和政策制定不能完全凭P是否小于一个特定的值来决定
重大决策与结论中,需要考虑诸多因素,如实验设计、数据质量、外部证据、假设的合理性等等,不能只由P值决定Yes or No的问题。
4. 正确的推理需要全面的报告和透明度
正确的科学推理,需要研究者公布研究中包含的所有假设,所有数据收集的决定,所有进行的统计分析和所有P值。
5. 一个P值,或者显著性,不能表示一个效应的大小,或者一个结果的重要性
P值大小不代表效应大小。再微小的效应,达到一定的样本量和测量精度,都能得到小的P值;再大的效应,在样本量和测量精度不那么高的时候,也可能只能得到普普通通的P值。
6. P值本身不能作为判断一个模型或假说的良好量度
单独的P值只能提供有限信息。用一个略小于0.05的P值来拒绝零假设就难以有说服力;相反,一个相对较大的P值也不能说就赞成零假设。当有其他方法可选时,数据分析不应该以一个简单的P值计算作为结束。